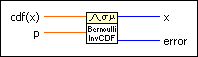
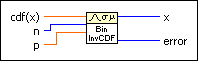
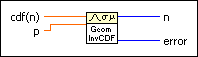
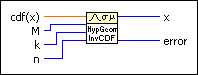
Discrete Inverse CDF VI

Owning Palette: Probability VIs

Requires: Full Development System

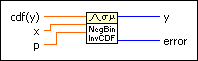
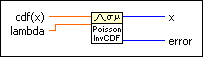
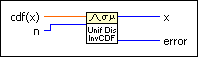
Computes the discrete inverse cumulative distribution function (CDF), or the value x such that the probability that the random variate X, where X describes the selected distribution type, takes on a value less than or equal to it is cdf(x). You must manually select the polymorphic instance to use.

Details  Example

Use the pull-down menu to select an instance of this VI.

Select an instance Bernoulli Inverse CDFBinomial Inverse CDFGeometric Inverse CDFHypergeometric Inverse CDFNeg Binomial Inverse CDFPoisson Inverse CDFUniform (Discrete) Inverse CDF

Add to the block diagram

Find on the palette

Bernoulli Inverse CDF

	cdf(x) is the cumulative probability Prob[X ≤ x].
	p is the probability of success (probability that x = 1) and must be in the interval [0,1].
	x is the number of successes, and will be either 0 or 1.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Binomial Inverse CDF

X represents a binomial-distributed variate: the number of successes in n independent Bernoulli trials. The Bernoulli probability parameter p is the probability of success of each trial or experiment.

	cdf(x) is the cumulative probability Prob[X ≤ x].
	n is the number of independent Bernoulli trials.
	p is the probability of success of each Bernoulli trial and must be in the interval [0,1].
	x is the number of successes and must be in the interval [0,n]
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Geometric Inverse CDF

X represents a geometric-distributed variate: given a sequence of n independent Bernoulli trials, X is the number of trials (or failures) before the first success. The Bernoulli probability parameter p is the probability of success of each trial or experiment.

	cdf(n) is the cumulative probability Prob[X ≤ n].
	p is the probability of success of each Bernoulli trial and must be in the interval [0,1].
	n is the number of independent Bernoulli trials.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Hypergeometric Inverse CDF

X represents a hypergeometric-distributed variate: the number of successes when n items are drawn from an M-sized population of which k elements are successes.

	cdf(x) is the cumulative probability Prob[X ≤ x].
	M is the number of elements in the population.
	k is the number of successes in the population.
	n is the number of items drawn without replacement.
	x is the number of successes out of the sample of n items drawn from the population.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Neg Binomial Inverse CDF

	cdf(y) is the cumulative probability Prob[X ≤ y].
	x is the number of successes and must be in the interval [0,inf].
	p is the probability of success of each Bernoulli trial and must be in the interval [0,1].
	y is the number of failures before the xth success.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Poisson Inverse CDF

X represents a Poisson-distributed variate which takes on discrete, non-negative values (X = 0, 1, 2, 3, ...) and often represents the number of events occurring within a specific time interval. The parameter lambda represents the average number of occurrences expected to occur within the specific time interval.

	cdf(x) is the cumulative probability Prob[X ≤ x].
	lambda is the average number of events expected to occur within a specific time interval.
	x is the number of events and must be greater than or equal to 0.
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Uniform (Discrete) Inverse CDF

	cdf(x) is the cumulative probability Prob[X ≤ x].
	n is the maximum value of the uniform variate.
	x is an integer in the range of [0,n].
	error returns any error or warning from the VI. You can wire error to the Error Cluster From Error Code VI to convert the error code or warning into an error cluster.

Discrete Inverse CDF Details

When using the Bernoulli instance of the VI, X represents a Bernoulli-distributed variate with one of two possible outcomes: success (x = 1) or failure (x = 0). The Bernoulli probability parameter p is the probability of success of a single trial or experiment.

Example

Refer to the Display Discrete Probability Distributions VI in the labview\examples\Mathematics\Probability and Statistics directory for an example of using the Discrete Inverse CDF VI.

 Open example  Find related examples