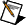Define PDE Domain VI

Owning Palette: Partial Differential Equations VIs

Requires: Full Development System

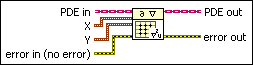
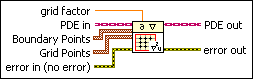
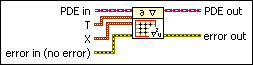
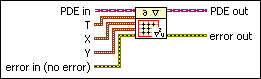
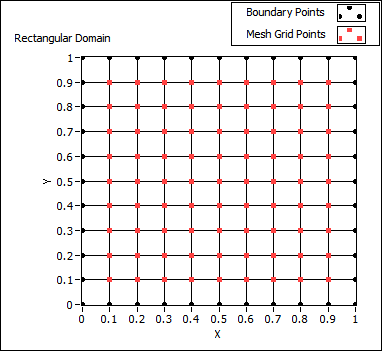
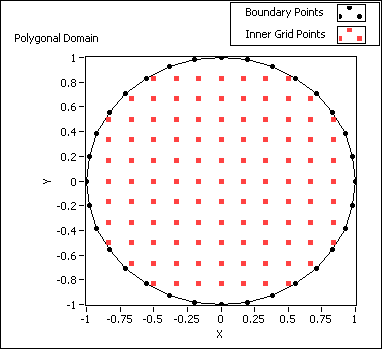
Defines the domain where you solve the partial differential equation. You must manually select the polymorphic instance to use.

Details  Examples

Use the pull-down menu to select an instance of this VI.

 Add to the block diagram  Find on the palette

2D Helmholtz (Rectangular domain)

PDE in is the class that stores the data of the equation.
X specifies the uniform mesh grid along the x-axis.
start x specifies the starting mesh grid point x0 along the x-axis. start x must be less than end x. The default is 0.
end x specifies the ending mesh grid point xm along the x-axis. end x must be greater than start x. The default is 1.
# of x-points specifies the number of grid points along the x-axis. # of x-points is equal to m + 1 and must be greater than 2. The default is 11.
Y specifies the uniform mesh grid along the y-axis.
start y specifies the starting mesh grid point y0 along the y-axis. start y must be less than end y. The default is 0.
end y specifies the ending mesh grid point yn along the y-axis. end y must be greater than start y. The default is 1.
# of y-points specifies the number of grid points along the y-axis. # of y-points is equal to n + 1 and must be greater than 2. The default is 11.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

2D Helmholtz (Polygonal domain)

grid factor specifies the density of the grid points that LabVIEW automatically generates. A smaller grid factor leads to denser grid points, which results in a more accurate solution but more computation time and memory. LabVIEW ignores grid factor if you wire a value to Grid Points. grid factor must be greater than 0 and less than 1. The default is 0.005.
PDE in is the class that stores the data of the equation.
Boundary Points specifies the boundary points that define a polygonal domain. The boundary points must be in a clockwise or counterclockwise direction. The number of points must be greater than 2.
X specifies the x-coordinate of Boundary Points.
Y specifies the y-coordinate of Boundary Points.
Grid Points specifies the grid points for the equation. The grid points must be in the polygonal domain. LabVIEW removes the points that are not in the polygonal domain. If you do not wire a value to Grid Points, LabVIEW automatically generates the grid points based on grid factor.
X specifies the x-coordinate of Grid Points.
Y specifies the y-coordinate of Grid Points.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

1D Heat

PDE in is the class that stores the data of the equation.
T specifies the uniform time steps.
initial t specifies the initial time step t0. initial t must be less than final t. The default is 0.
final t specifies the final time step tl. final t must be greater than initial t. The default is 1.
# of t-points specifies the number of time steps. # of t-points is equal to l + 1 and must be greater than 1. The default is 11.
X specifies the evenly spaced points along the x-axis.
start x specifies the starting point x0 along the x-axis. start x must be less than end x. The default is 0.
end x specifies the ending point xm along the x-axis. end x must be greater than start x. The default is 1.
# of x-points specifies the number of points along the x-axis. # of x-points is equal to m + 1 and must be greater than 2. The default is 11.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

2D Heat (Rectangular domain)

PDE in is the class that stores the data of the equation.
T specifies the uniform time steps.
initial t specifies the initial time step t0. initial t must be less than final t. The default is 0.
final t specifies the final time step tl. final t must be greater than initial t. The default is 1.
# of t-points specifies the number of time steps. # of t-points is equal to l + 1 and must be greater than 1. The default is 11.
X specifies the uniform mesh grid along the x-axis.
start x specifies the starting mesh grid point x0 along the x-axis. start x must be less than end x. The default is 0.
end x specifies the ending mesh grid point xm along the x-axis. end x must be greater than start x. The default is 1.
# of x-points specifies the number of grid points along the x-axis. # of x-points is equal to m + 1 and must be greater than 2. The default is 11.
Y specifies the uniform mesh grid along the y-axis.
start y specifies the starting mesh grid point y0 along the y-axis. start y must be less than end y. The default is 0.
end y specifies the ending mesh grid point yn along the y-axis. end y must be greater than start y. The default is 1.
# of y-points specifies the number of grid points along the y-axis. # of y-points is equal to n + 1 and must be greater than 2. The default is 11.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

1D Wave

PDE in is the class that stores the data of the equation.
T specifies the uniform time steps.
initial t specifies the initial time step t0. initial t must be less than final t. The default is 0.
final t specifies the final time step tl. final t must be greater than initial t. The default is 1.
# of t-points specifies the number of time steps. # of t-points is equal to l + 1 and must be greater than 1. The default is 11.
X specifies the evenly spaced points along the x-axis.
start x specifies the starting point x0 along the x-axis. start x must be less than end x. The default is 0.
end x specifies the ending point xm along the x-axis. end x must be greater than start x. The default is 1.
# of x-points specifies the number of points along the x-axis. # of x-points is equal to m + 1 and must be greater than 2. The default is 11.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

2D Wave (Rectangular domain)

PDE in is the class that stores the data of the equation.
T specifies the uniform time steps.
initial t specifies the initial time step t0. initial t must be less than final t. The default is 0.
final t specifies the final time step tl. final t must be greater than initial t. The default is 1.
# of t-points specifies the number of time steps. # of t-points is equal to l + 1 and must be greater than 1. The default is 11.
X specifies the uniform mesh grid along the x-axis.
start x specifies the starting mesh grid point x0 along the x-axis. start x must be less than end x. The default is 0.
end x specifies the ending mesh grid point xm along the x-axis. end x must be greater than start x. The default is 1.
# of x-points specifies the number of grid points along the x-axis. # of x-points is equal to m + 1 and must be greater than 2. The default is 11.
Y specifies the uniform mesh grid along the y-axis.
start y specifies the starting mesh grid point y0 along the y-axis. start y must be less than end y. The default is 0.
end y specifies the ending mesh grid point yn along the y-axis. end y must be greater than start y. The default is 1.
# of y-points specifies the number of grid points along the y-axis. # of y-points is equal to n + 1 and must be greater than 2. The default is 11.
error in describes error conditions that occur before this node runs. This input provides standard error in functionality.
PDE out returns PDE in with the domain.
error out contains error information. This output provides standard error out functionality.

Define PDE Domain Details

The following illustration shows the uniform mesh grid on a rectangular domain with the default values. Both the x- and y-axes range from 0 to 1 with 11 evenly spaced grid points. The black circle points are the points on the boundary of the rectangular domain. The red square points are the inner points on the mesh grid.

The following illustration shows the unit circle on a polygonal domain. The black circle points are the points on the boundary of the domain that generate evenly on the unit circle. The red square points are the inner grid points that generate automatically with the default of grid factor.

You must specify the boundary points in a clockwise or counterclockwise direction.

The following block diagram illustrates a VI that defines the polygonal domain, as shown in the previous illustration.

If you do not wire a value to Grid Points, LabVIEW generates the boundary points automatically based on grid factor, which determines the density of the grid points. LabVIEW performs triangulation on the grid points before solving the equation. The grid factor approximates the ratio of the average area of the triangles to the area of the whole polygonal domain.

If you have prior knowledge of the unknown function, wire a value to Grid Points. You can use sparse grid points in areas where the unknown function varies smoothly and use dense grid points in areas where the unknown function varies sharply. For some problems, this flexibility in the choice of grid points can return better results than a set of uniformly distributed grid points.

Examples

Refer to the following VIs for examples of using the Define PDE Domain VI: