Chebyshev Polynomial VI

Owning Palette: Orthogonal & Non-orthogonal Polynomials VIs

Requires: Full Development System

Calculates the Chebyshev polynomial of order n at the point x.

Details  

Add to the block diagram

Find on the palette

	x is any real number.
	n is the nonnegative order (integer) of the Chebyshev polynomial.
	T(n,x) is the value of the nth Chebyshev polynomial at the point x.

Chebyshev Polynomial Details

The following equation defines the Chebyshev polynomial T_n(x).

T_n(x) = cos(n arccos(x)) for n = 0, 1, 2, ..., and real numbers x.

Note  The result of this definition does not look like a polynomial at first glance, but you can use trigonometric rules to show that Tn is a polynomial of degree n in the variable x.

T_n(x) forms the base of the Chebyshev approximation. For i j, the following equation gives the Chebyshev approximation.

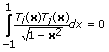
All T_n(x) form an orthogonal system over the weight function

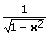
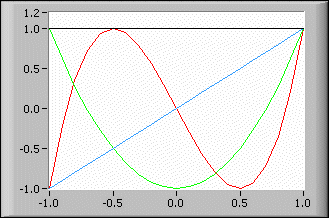
The following illustration shows the graph for the first four Chebyshev polynomials of degrees 0, 1, 2, and 3.